▶ を押すと文が増えます
「算法少女」に出てくる問題を解いてみよう!
問題
半円に直角三角形を内接させ、この直角三角形の内接円と、弓形内にえがいた最大の円があいひとしいときの外接円と小円の半径の関係を問う問題である。
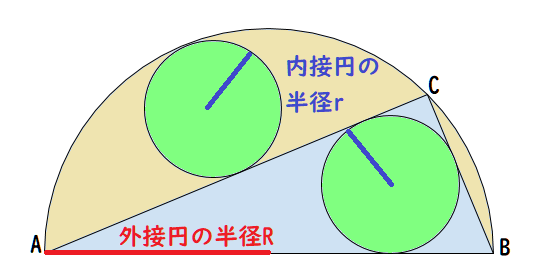

外側にある大きな円(外接円)の半径Rと、等しい2つの内接円(小円)の半径rの関係を数式で表すように求めている問題ですね。
えすとれの解法
1.内接円の半径を求める公式を使ってゴールを決める

せっかく「内接円」と書かれているので、公式を使って表してみましょう。
『三角形の面積の2倍 = 内接円の半径 × 三角形の三辺の総和』 です。
公式の証明はリンク先を参考にしてください。
以降、線分BCの長さをa、ACの長さをb、ABの長さをcと表す。
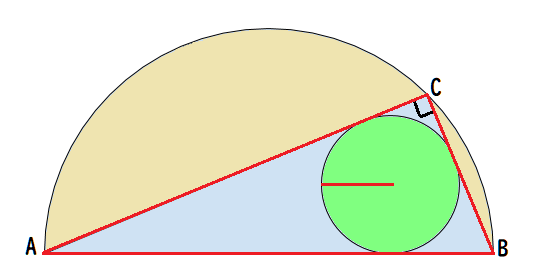
三角形ABCは直角三角形であるから、
三角形の面積の2倍 = a × b
三角形の辺のうち、cは円の直径に等しいので
c = 2R
ab = r ( a + b + 2R )

aとbを求めて、この式に代入すれば答えが出せそうです!
2.aの長さをRとrで表す

次は、三角形の外側にある小円に注目します。
外接円の中心Oから、円周にむかって線分BCと平行な直線を引く。線分ACとの交点をD、円周との交点をEとする。
三角形ABCと三角形AODは、角Aを共有しBCとODが平行であるから、相似である。また、点Oが円の中心であることにより、AO = OB = Rとわかり、AO : AB = 1 : 2が導かれる。
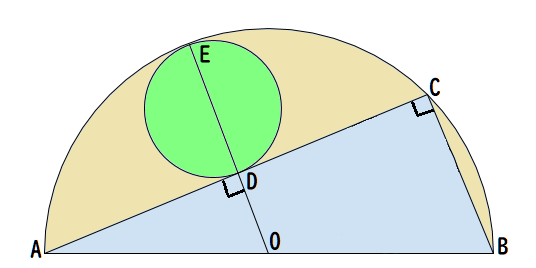
三角形AODと三角形ABCの相似比が 1 : 2 であるから、
OD = a ÷ 2
線分DEは内接円の直径であるから、
DE = 2r
線分OEは外接円の半径でもあるため、
OE = R
R = 2r + ( a ÷ 2 )
全体に2をかけて、2R = 4r + a
aを求める式になるよう移項して、
a = 2R – 4r
3.bの長さをRとrで表す

再び、三角形の内接円に注目します。
内接円の中心をPとおく。頂点Aと頂点B、それぞれからPまで角の二等分線を引く。Pから線分ABへ垂直に線を引き、交点をFとする。BC、ACについても同様に行い、交点をG、Hとする。
三角形AFPと三角形AHPは合同であり、三角形BFPと三角形BGPもまた合同である。四角形PGCHは、すべての角が直角であり、隣り合う辺のPG、PHがどちらも内接円の半径rに等しいことから、正方形である。
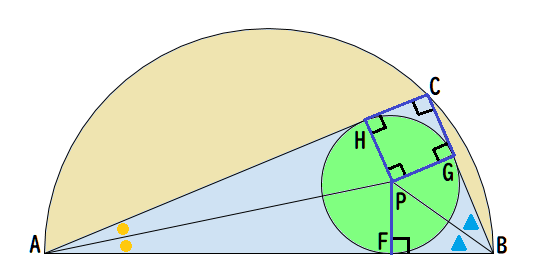
2.の計算結果より、
a = 2R – 4r = r + GB
GB = 2R – 5r
合同な三角形の性質よりGB = BFであるから
2R = AF + 2R – 5r
AF = 5r
同様に、AF = AHであるから
b = 5r + r
b = 6r
4.答えを求める

必要なピースはすべて揃いました! 代入して答えを求めましょう!

1.より ab = r ( a + b + 2R )
2.より a = 2R – 4r
3.より b = 6r
(2R – 4r) × 6r = r ( 2R – 4r + 6r + 2R)
全体をrで割ってから計算
12R – 24r = 4R + 2r
8R = 26r
4R = 13r
答えは『外接円の半径の4倍が、内接円の半径の13倍に等しくなる』
別解:ゴールを三平方の定理にする

1.で設定するゴールの式は、三平方の定理を使っても解くことができます。直角三角形ならば、直角を挟む2辺をそれぞれ2乗したものの和が、斜辺の2乗に等しくなるというものですね。内接円の半径の公式の方が、表現が簡素になったのでそちらを選択しました。
「算法少女」には、他にもユニークな問題が登場します。是非読んで、取り組んでみてくださいね。


